회로 해석을 하는 데 있어서 한 개의 작은 블락은 대신호 모델에서 small signal parameter를 구하는 방법으로 해석할 수 있습니다. 하지만 Transmitter 나 Receiver 그리고 다른 여러 개의 블락이 합쳐진 회로에서는 일일이 하나의 소신호를 구할 수 없습니다. 각 블락의 gain 과 dynamic range 등을 파악하고 이를 제어공학에서 배운 방법을 통해 해석합니다. 하지만 이 제어공학의 전제에는 아주 중요한 전제가 깔려있는데요, 그것은 바로 각 블락이 linear하다는 전제입니다.
그렇다면 Linear하다는 것은 무슨 뜻일까요?
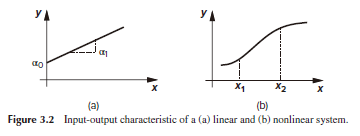
어떤 시스템이 linear 하다는 것은 input 에 따라 output 이 linear 하게 변하는 것을 의미합니다. (a) model 을 보면 input 과 output의 관계가 일정한 기울기를 갖는 직선임을 알 수 있습니다. 따라서 두 점의 값을 알면 모든 input 에 대한 output 값을 알 수 있죠! (두 개의 점을 알면 직선의 기울기와 y절편을 알 수 있으니까요) 하지만 (b) 의 non-linear 한 시스템을 보겠습니다. input 과 output 의 관계가 일정하지 않고 곡선을 이루고 있기 때문에 두개, 아니 그 이상의 값을 알아도 새로운 input이 들어온다면 output을 정확히 알 수 없죠. 단순히 여러 개의 input 으로 output 을 추정할 수 있을 뿐입니다. 이와 같이 회로에서는 unknown 상태를 매우 싫어합니다. 따라서 회로를 분석할 때 충분히 linear 하다고 "가정" 을 하고 해석하게 됩니다.
하지만 실제로 회로, 아니 1개의 mosfet은 linear 할까요?
당연히 아닙니다. 회로는 정말 당연하게도, 전자회로의 맨 첫장부터 linear 하지 않습니다.

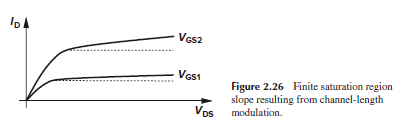
회로 해석에서 가장 정석적인 방법은 small signal model로 분석하는건데요, 어느 한 DC 포인트에서 small signal parameter를 구하고 아주 작은 input 에 대해 이 parameter가 고정되있다는 가정이 깔려있습니다. 하지만 Amplifier 의 input 은 생각보다 크게 들어오고, 이 input 에 따라 사실 small signal parameter는 매순간 바뀌어야겠죠. 대신호적으로 해석하더라도 실제 Channel-length modulation 과 Body effect 등의 현실적인 문제들 때문에 input 과 output 의 단계는 linear 하지 않습니다.
여기서 살짝 옆으로 비껴나가 Fast Fourier Transform, FFT 에 대해 알아봅시다.
기존의 공업수학에서 Laplace transform 과 Fourier transform 에 대해 배우는데요, FFT 는 finite 한 신호 (길이가 유한정한)에 대해서도 분석을 할 수 있는 아주아주 강력한 도구입니다. 아~~주 간단하게 말한다면 2ns의 신호가 들어온다고 가정해봅시다.

2ns 동안 이 신호는 아주 완벽한 sine wave 를 그리며 들어왔습니다. 그러면 우리는 이 신호를 1GHz 의 sine wave 라고 볼 수 있을까요? 이 신호는 (a) 처럼 2ns 가 지난후에 의미없는 노이즈가 나올수도 있습니다. 반면에 (b) 처럼 깨끗한 1ns 의 주기를 가지는 sine wave가 계속 나올수도 있죠. 신호 해석을 더 간단히 하기 위해서는 (a)가 편할까요 (b) 가 편할까요? 당연히 (b) 입니다. 저희는 유한한 signal (2ns 의 sine wave) 이 무한히 반복된다는 가정하에 signal 을 해석하게 됩니다. 이렇게 무한히 일정 주기를 갖고 반복하는 signal 이 있을 경우 시간 영역이 아닌 주파수 영역에서 해석이 가능하게 됩니다.
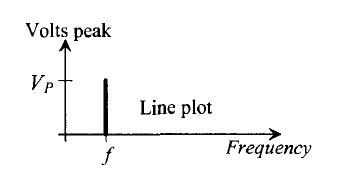
위에서 보이는 것과 같이 특정 주파수, 이 경우에는 1GHz 에서 크기만 갖는 impulse 함수를 Frequency 영역에서 보여주게 될 것입니다. 이 FFT 의 경우 signal 을 분석하는 데 정말 강력한 도구가 됩니다. 왜냐하면 유한한 어느 신호라도 무한히 반복된다는 가정하에는 주파수 영역에서 해석이 가능하기 때문이죠!!

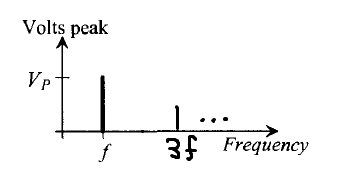
시간 영역에서는 아주 완벽한 sine wave 처럼 보이지만 주파수 영역에서는 이렇게 주파수의 2배, 3배, .... , n배에서 찌꺼기들이 낄 수 있기 때문이죠. 이러한 찌꺼기들을 harmonic 성분이라고 부르며, 이는 모두 회로의 non-linear 한 특성 때문에 생기게 됩니다. 따라서 전체 시스템 설계자 입장에서는 linearity 에 대한 스펙도 잘 고려해서 짜야하죠. PLL, ADC, Amplifier 등 모든 analog block은 linearity 라는 특성을 고려해야합니다.
그렇다면 이러한 회로의 linearity 특성을 향상시키는 방법은 무엇이 있을까요?
가장 간단하면서 효과적인 방법은 바로 differental 회로를 이용하는 것입니다. Differential 회로는 + input 과 - input , 즉 같은 amplitude 를 갖지만, 부호가 다른 신호를 이용하는 건데요, 이 방법을 통해서 non linear 한 성분 중 짝수 찌꺼기를 제거할 수 있습니다(even-order harmonic). 따라서 Differential 방식은 회로의 output dyanmic range 를 effectively 2배를 늘림과 동시에 짝수 찌꺼기를 제거해 linearity 또한 개선할 수 있는 사기 테크닉인거죠!
다른 방법으로는 무엇이 있을까요? 또 간단한 방법으로는 Source degeneration을 이용하는 것입니다.

Mosfet의 source 쪽에 저항을 추가함으로써 회로의 linearity 를 쉽게 개선할 수 있습니다. 이는 input 에 따른 output 의 gain이 작아지기 때문입니다. 이러한 작은 gain으로 인해 같은 input 에 대해 output 이 더 조금 스윙하게 되고 결국 linearity 성분이 좋아지게 됩니다. 결국 gain 을 trade-off 하여 linearity를 얻어낸 것이죠! 따라서 Gain이 높으면서 linearity 성분이 좋은 amplifier 를 설계하는 것은 매우 힘들다는 반증이기도 합니다.
또다른 방법으로는 Look-up table을 만들어 회로의 linearity 를 개선할 수 있는 방식입니다. Look up table은 따로 input 과 output의 관계를 미리 알아내어 input 에 대한 옳은 output을 내보내는 간단한 회로입니다. 실제로 calibration이 적용되지 않은 여러 논문에 나온 회로들이 이 look-up table 방식을 이용하죠. 따로 look up table 을 만들어야 하고 이를 update해야한다는 단점이 있습니다.
이상입니다.
'반도체 > 전자공학 기초' 카테고리의 다른 글
| Common source stage 에서의 Source degeneration (0) | 2023.05.07 |
|---|---|
| Diode란? (1) depletion region, drift & diffusion current, forward & reward bias (0) | 2023.04.23 |
| 5-2. Miller cap compensation (2) | 2023.01.14 |
| 6. Current mirror (0) | 2023.01.08 |
| 5-1. Amplifier의 gain을 늘려야하는 이유 (0) | 2023.01.07 |
