
오늘은 회로를 설계하는 데도 중요하고, 시스템 레벨에서는 필수적이라고 할 수 있는, 가장 강력한 회로 분석 기술인 Fast fourier transform 에 대해 다뤄보겠습니다. FFT 에 대해 엄밀하게 다루는 방법이나 수식 전개 방법 등은 예제들을 풀고 직접 시스템을 분석하면서 익힐 수 있으므로, 이번 글에서는 대략적인 개념에 대해 건드리는 방식으로 진행해보겠습니다.
Fast fourier transform 은 우리나라 말로 고속 푸리에 변환이라고 하며, 아주 간단하게 생각하면, 함수의 근삿값을 계산하는 알고리즘입니다. 함수의 근삿값이라고 하니 잘 와닿지 않습니다. 좀만 더 이해하기 쉽게 말하면 우리가 설계한 회로에 어떠한 input signal 이 들어올 때, 이 input signal 에 여러가지 조건을 가정해 미래 신호를 예측하는 것입니다. 아래 간단한 예로 시작해보죠.

보통 전자회로 시간에 amplifier 부터 배우게 되는데요. 일반적으로 amplifier 에는 위와 같은 sine wave 를 input 으로 넣게 됩니다. 이 때 우리가 가정하는 조건이 있는데요. 바로 이 input 신호가 시간에 상관없이 sine wave 라는 가정을 하게 되죠. (혹은 우리가 관심있어 하는 시간동안에는) 하지만 실제 생활에서 우리가 들어오는 신호는 저럴리가 없죠.

특정 시간에는 ideal 한 sine wave 형태를 띄더라도 특정 시간이 지난 후에는 지글지글 자기 멋대로 움직이는 신호일 수 있죠. 결국 FFT를 하는 데 가장 중요한 조건이 바로, 특정 신호를 분석할 때 우리가 관심있어 하는 시간대를 설정하고 이 신호는 해당 시간을 주기로 갖는 신호라는 가정입니다.
가장 기초적이지만 필수적인 조건을 알았으니 FFT 는 사실 간단합니다. 어느 신호가 들어오든간에, 그 신호가 주기를 갖고있는 반복적인 신호라고 가정했으니, 이제 신호는 단순 시간 영역에서만 분석할 수 있는 것이 아닌, 주파수 영역에서도 분석할 수 있죠.
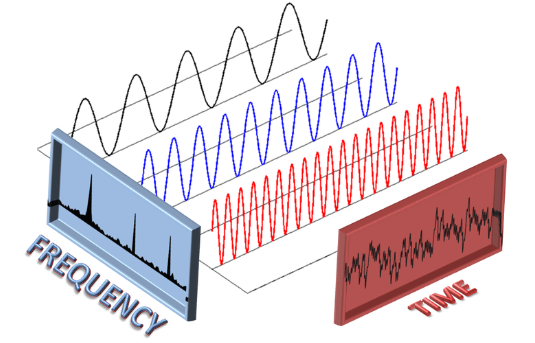
위대한 수학자들과 과학자들이 증명해놓은 것이 있는데요. 특정 신호가 무한히 반복한다고 가정하면, 그 신호가 아무리 규칙성이 없어보이는 랜덤해 보이는 신호더라도, 수많은 sine wave 의 합으로 그 신호를 나타낼 수 있다는 것입니다. 바로 위가 그 예를 보여줍니다. 빨간색의 신호는 언뜻 보기에는 마구 흔들리는 아무 규칙없는 신호같지만, FFT 를 이용한다면 수많은 sine wave 합으로 그 신호를 구현해낼 수 있죠. (그리고 이 sine wave 조합은 unique 합니다.)
그러면 어떻게 생긴 신호냐에 따라서 주기가 2인 sine wave 성분으로 크게 구성될 수도 있고, 주기가 7인 sine wave 성분으로 크게 구성될 수도 있습니다. 여기서 주기는 결국 뭐죠? "주기 = 1/주파수" 로 결국 어떤 주파수의 sine wave 성분이 그 신호를 구성하는 데 더 큰 영향을 주냐~ 를 나타낸 것이 바로 FFT 를 사용한 frequency domain 입니다.
바로 이 FFT 를 사용해 frequency domain 으로 신호와 시스템을 해석하게 된다면, 시간으로 분석할 때 보다 훨씬더 많은 정보를 얻을 수 있습니다. input 으로 pure 한 sine wave 를 넣고 output 에 어떤 신호가 나오는지를 분석해서 시스템의 linearity 를 알수도, ADC 와 DAC 의 resolution 을 알수도, 회로가 noise 에 얼마나 robust 한지도 알 수 있습니다. 이러한 것들은 time domain 에서 알기 상당히 힘든 정보들이죠. FFT 를 어떻게 계산하고, 수식을 전개하는 것도 매우 중요합니다만, FFT 가 어떻게 활용되는지, 왜 배워야하는 지를 이해하는 것이 필수입니다. 이상입니다.
'반도체 > 전자공학 기초' 카테고리의 다른 글
| Logic gate 로직 게이트 쉽게 분석하는 방법 (0) | 2024.09.03 |
|---|---|
| MOSFET 특성 : Input impedance 와 parasitic cap (0) | 2024.06.21 |
| 회로의 dynamic range : Circuit dynamic range (0) | 2024.06.06 |
| MOS differential pair : 세가지 분석으로 완벽하게 파헤치기 (1) | 2023.10.23 |
| Feedback system : 회로의 제어공학적 해석과 전제 조건 (0) | 2023.10.20 |
